Again Computers and the Brain
- heterarchy, poly-contexturality, neural nets, brain, computer -
R.Kaehr and E. von Goldammer
Abstract
Theoretical analyses of the logical structure for an adequate ´theory of living systems´ reveal the shortcomings of all standard logical systems ranging from two-valued Aristotelian logic to n-valued types eulogized by Post, Lukasiewicz and others. All these calculi have one thing in common that makes them completely inadequate for any formalization of self-referential systems, i.e., all living systems; they are essentially linear. ´Linear´ in the technical sense of being one-dimensional, since all logical statements are arranged in an ordered, unique sequence of numbers, resulting in pure hierarchically structured organizations. Self-reference, however, derives only from heterarchical structured Systems. Günther developed a formal, codifiable system of mathematical logic (´theory of poly-contexturality´) which goes beyond all multi-valued logics that have been common up to now, and possesses the ability to describe heterarchically structured systems in a formal mathematical sense. In other words, the ´theory of poly-contexturality´ provides the theoretical basis for simulating self-reflecting processes (cognition) on logical machines. The subject is considered in connection with McCulloch´s study on a heterarchy of values determined by the topology of nervous nets.
INTRODUCTION
One goal in brain research is to separate the mechanisms of biological information processing and intelligence of living systems from neurophysiological processes, in the vague hope of one day understanding the whole range of behavior in animals and/or man in terms of the structure-function relationships of the neural circuitry of their central nervous systems. The construction of intelligent devices, on the other hand, is the declared aim of the artificial intelligence (AI) sciences.
Despite the differences, there are certain connections between both scientific fields, resulting in a permanent mutual influence which reached one of its summits with the logification of neural activities by McCulloch and Pitts /1/ in their famous study, ´A Logical Calculus of the Ideas Immanent in Nervous Activity´, a model which still acts as a paradigm in neurosciences. The present study does not intend to question this paradigm, but to point to the possibilities of its evolution.
Many modern neuroscientific research findings can no longer be described in a reductionistic and hierarchical way. In particular, self-referentiality, an attribute which characterizes all complex neural networks, cannot be described adequatly either through the Von Neumann computer model or through the McCulloch-Pitts model.
It was not the intention of this study to grasp the brain conceptually using the notions of computer sciences, i.e., to consider the brain as a computer, but to focus attention on the consequences resulting from considering the Computer as a brain as has been discussed by biological scientists. In this context we refer to the work of von Foerster /2/, Löfgren /3/, Maturana and Varela /4/ and Günther /5/. The conception of Günther´s /6,7/ ´poly-contexturality´ will the basic reference source throughout this paper.
It has scarcely been noticed in the scientific literature that shortly after ´A Logic Calculus …´, had been published, McCulloch presented a paper entitled ´A Heterarchy of Values Determined by the Topology of Nervous Nets´ /8/, in which he pointed to the necessity of introducing non-transitive and heterarchical structures for an adequate description of neural activities. However, because of their irreducible topological distribution, heterarchical structures elude any logification in the classic logical frame of relations - this is the problem. Later, in a lecture ´What´s in the Brain that Ink May Character?´/9/. McCulloch again clearly pointed out this general logical problem.
HIERARCHY versus HETERARCHY
Based on its logical assumptions, the Von Neumann machine is exclusively linear and hierarchically structured and excludes any circularity in a fundamental logical sense. A graphic metaphor for such a structure is given by the tree as represented, e.g., by the binary decision tree. Although parallel computers have to be considered as non-Von Neumann machines, they are still hierarchically organized, because the classic-logical rules are rigorously valid, viz., the law of transitivity or the exclusion of self-referentiality. Their data and algorithmic structures are reducible to one and only one comprehensive logical fundament as an operational ´universe of discourse´. This is shown, for example, by an analysis of the methods of modeling and formalizing non-Von Neumann architectures by Petri-Holt nets and the normalized nets of Rödding /10/.
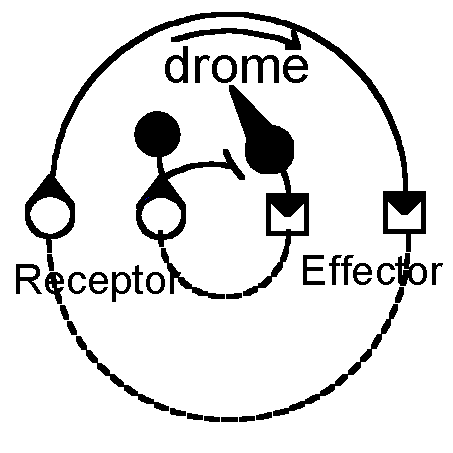
In the following discussion, McCulloch´s nervous nets as they are represented by the figures in Ref. 8 will be analyzed. Fig. la here depicts the simplest model of a circular propagation of neural stimulations. According to the Bell-Magendie law, the nervous excitations enter the nervous system by dorsal and emerge by ventral roots. Circular propagation in this direction was called dromic and that in the opposite direction antidromic. So far no response of any effector has ever indicated an antidromic reflex, although conduction in the reverse direction has been demonstrated in both dorsal and ventral roots. All reflexes are dromic activities of feedback mechanisms with reverberating circuits (the endromes), which are not shown in Fig. 1. These feedback circuits, i.e., both endromes and reflexes, may be regenerative for one temporal combination of excitations and degenerative for another. Further details may be found in the work of McCulloch and Pitts /1/.
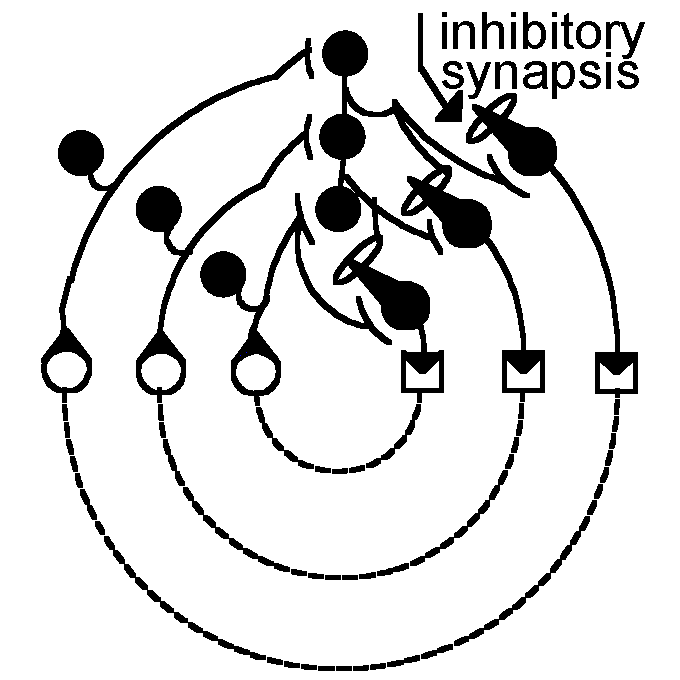
If an arbitrary number of parallel nervous circuits are considered, the conduction in each is dromic, in two or more syndromic, but from one to the other, whether it facilitates or inhibits, it is neither syn- nor anti-, but heterodromic. Without heterodromic activity, reflexes would occur independently of one another or, to put it in other words, for any sub-, super- or co-ordination of reflexes heterodromic activity is inevitable. In this way an inhibiting influence from one circuit to the other can be exerted. The resulting network maps are indicated in Fig. lb.
 |
 |
 |
( a ) |
( b ) |
( c ) |
| Figure 1: Neural
nets, from Ref. 8 continuous line : nervous portion of path; broken line : nervous somatic or environmental protion of path. |
||
|
b) parallel and hierarchic
|
c) heterarchic
(non-transitive)
|
The heterodromic configuration in Fig. 1b is isomorphic with that of the parallel computers mentioned above and, like those, it is hierarchically structured. This can be expressed in a more logical notation. For three neural processes A, B and C (as in Fig. 1b), if A is preferred to B and B to C, it follows that A is preferred to C, viz.,
|
(1) |
Relation (1) reflects the validity of the transitivity law of the classic-logical implication postulated for a hierarchy of values or processes which only admit a notion of super- or sub-ordination but no co-ordination. This, however, contradicts observations of neural processes such as the coordination of visual, tactile and/or acoustic perception.
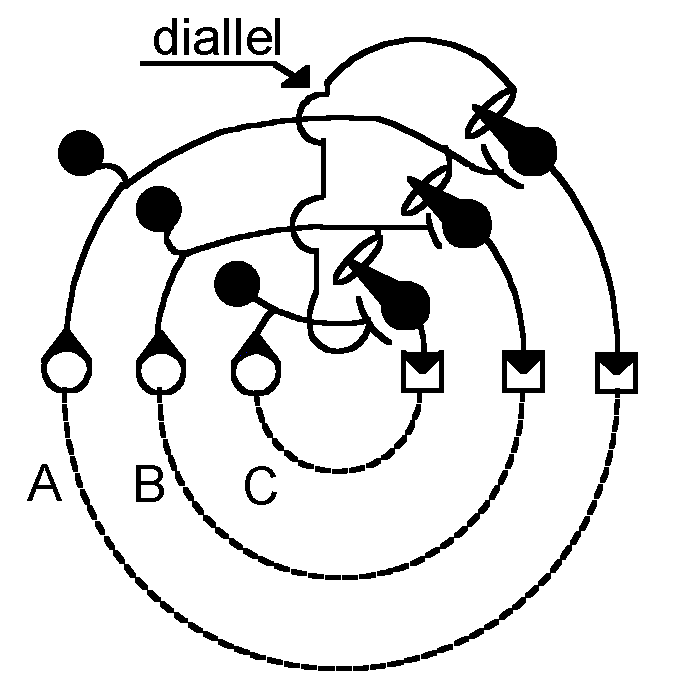
Figure 1c illustrates the simplest (irreducible) nervous net with a ´diallel´ linking of the dromes such that the classic-logical transitivity for the preference relation (1) no longer holds, viz.,
|
(2) |
It should be
mentioned that the relation ![]() neither follows from Fig. 1c nor
was it discussed by McCulloch; here it has been added for sake of
completeness. The net in Fig. 1c can no longer be reproduced on a
plane such as is always possible in principle for parallel
structures (cf. Fig. 1b). The simplest surface on which this net
can be mapped topologically is a torus, which means that a
twofold closure of the net results (cf. von Foerster /2/). For clarification, it should be added that the
notion ´diallel´, as it was used by McCulloch /8/, is a logical (scholastic) term pointing toward a ´circulus
vitiosus´.
neither follows from Fig. 1c nor
was it discussed by McCulloch; here it has been added for sake of
completeness. The net in Fig. 1c can no longer be reproduced on a
plane such as is always possible in principle for parallel
structures (cf. Fig. 1b). The simplest surface on which this net
can be mapped topologically is a torus, which means that a
twofold closure of the net results (cf. von Foerster /2/). For clarification, it should be added that the
notion ´diallel´, as it was used by McCulloch /8/, is a logical (scholastic) term pointing toward a ´circulus
vitiosus´.
McCulloch /8/ introduced the term ´heterarchy´ and delimitated it very clearly from the concept of a circulus vitiosus founded in the linearity, a concept used later for modeling living systems in connection with the indefinite recourse of operations by von Foerster /2/ and Varela /11/.
The concept of the logical diallel combines both non-transitivity (circularity) and heterarchy, i.e., the co-ordination of domains or values which cannot be submitted to a summum bonum. The diallel allows circularity on the roundabout of changing dimensions in a complex topology of domains without relapsing into the self-reflection of a circulus vitiosus.
Since within any domain the hierarchical principle holds and the multitude of domains are combined by the principle of heterarchy, systems structured in this way allow an interplay of coordination (heterarchy) and sub ordination (hierarchy).
It is the distribution of qualitatively different domains which has no equivalent in classical logic where a single basic domain is classified in types, categories, worlds, etc. This is the fundamental difference between McCulloch´s conception of heterarchy and that of the so-called ´radical constructivism´/12/.
Under these conditions it is no longer possible to submit a nervous net (in the sense of McCulloch) to one and only one super-ordinated logical aspect or concept. That means that modeling and formalization of heterarchical structures, which have to be considered as system-wholes or complex systems, require a multiplicity of simultaneous points of view.
If non-transitivity has to be modeled within the framework of the classical logic, antinomic situations will be generated as is expressed, for example, by relation (2). Therefore, the question arises of how a complex system can be unambiguously described with the indicated structural features in a consistent formal logical way.
The brain is a self-referential system par excellence. It always interacts with its own states, i.e., it is a completely closed system equipped with neither a sensorium (sensory cells) nor a motorium (muscles) - its boundaries are given by the boundaries of the nervous nets. The fact that its activity may be changed by stimulated sensory cells and that it may act on glands or muscles is a phenomenon which exists only for an observer and not for the brain itself /4,13, 14/.
All stimulations of the sensorium, whether they arc exo- or endo-somatic, are codified (at the receptor cells) and transmitted (in the neural net) as quantities and only as quantities. It is in the brain (and not at the sensory cells) where all impressions (colors, smell, etc.) and sensory perceptions (even of one´s own body) are reckoned from those quantities, i.e., where the change from quantity to quality takes place.
All functions of the brain always result from interacting nervous nets, which are located in specific domains of nearly all parts of the brain. They are never the result of isolated single centers and even less the result of a summum bonum. The emphasis is placed on the interaction of topologically different specific domains, such as the thalamo-cortical system, the limbic system and the ascending reticular activating system. These three systems are known to be essential for the capability of the brain to become self-conscious (self-referentiality). All three represent large nervous circularities closely interwoven with each other, i.e., from a structural point of view the situation resembles the heterarchical model in Fig. 1c, with all the logical complications required for an adequate description. On the logical side, this heterarchical structure can be modeled using the ´theory of poly-contexturality´.
To summarize, nervous nets are systems characterized _1) by the topological distribution of different interacting centers and interacting circularities; _2) by non-transitivity of nervous activities; and _3) by self-referentiality of their organization. As McCulloch showed in his study ´What´s in the Brain ... ?´, /9/ the treatment of this subject does not belong to the field of neurophysiology but represents a general logical problem which requires a new logical conception. McCulloch himself has been involved in developing a triadic logic (´logic triadas´) /15/.
Contrary to the linguistic frame of the classical logic, which does not admit any consistent description of self-referential, non-transitive processes and distributed irreducible domains, the theory of poly-contexturality with its conception of distribution and mediation of domains offers an adequate logical tool for a consistent formalization of complex systems. This will be demonstrated briefly using the example of non-transitivity from Fig. 1c. For the sake of simplicity this will be accomplished by a poly-contextural interpretation of multi-valued logic. Continuative conceptions have been elaborated by Kaehr /16/.
As is well known, classical logic is two-valued. Multiple-valued logical systems extend the two-valuedness by introducing intermediate values which are arranged between the two classical truth values. The domain, which can be described by a two-valued logic or a classical multiple-valued logic, will be called a contexture.
PoIy-contexturality originates as follows:
classical logic is defined between any two
values resulting in a contexture; in a case with three values,
however, where the third is not placed between
´true´ and ´false´ but beyond
´true´ and ´false´, three two-valued logical systems are
generated to which three contextures are assigned. Four values
define six logical domains, and in general, with m
values ![]() two-valued logical systems are created. The logical systems or
contextures defined in this way do not coexist in isolation but
are mediated with each other. Figure 2 illustrates the situation
for three logical systems L1,2,3 corresponding to McCulloch´s heterarchically
structured model as shown in Fig. lc, a model which is an
irreducible representation of a nervous net with a linking
diallel.
two-valued logical systems are created. The logical systems or
contextures defined in this way do not coexist in isolation but
are mediated with each other. Figure 2 illustrates the situation
for three logical systems L1,2,3 corresponding to McCulloch´s heterarchically
structured model as shown in Fig. lc, a model which is an
irreducible representation of a nervous net with a linking
diallel.
As can be seen from the pattern in Fig. 2, the
exchange relation causes ambiguity between the logical terms
´true´ and ´false´. This scheme corresponds to a
three-contextural logical system, the lowest meaningful
contexture in the poly-contextural theory. In order to illustrate
the difference between a classical two-valued logic and the
multiple-valuedness of a compound contexture, such as that
presented in Fig. 2, the truth table for the conjunction ![]() , the disjunction
, the disjunction ![]() , the implication
, the implication ![]() ,
and the two negations (N1,2) will be exemplified briefly. The way in which the
order and exchange relation have to be assigned into the general
formalization will not be discussed here.
,
and the two negations (N1,2) will be exemplified briefly. The way in which the
order and exchange relation have to be assigned into the general
formalization will not be discussed here.
|
| Figure 2 : Three logical
systems (domains), L1,2,3. T : true; F : false; -->: order relation; >--< : exchange relation --- : coincidence relation. |
Table 1 represents a truth table for a three-contextural logic. In order to simplify the notation, the following abbreviations have been introduced, which immediately become clear if they are compared with the symbols in Fig.2:
|
(3) |
( a ) |
( b ) |
|||||||||||||||||||||
L1 |
L2 |
L3 |
L1 |
L2 |
L3 |
|||||||||||||||||
X1 |
Y1 |
X2 |
Y2 |
X3 |
Y3 |
|
|
|
||||||||||||||
T1 |
T1 |
T3 |
T3 |
T1 |
T3 |
|||||||||||||||||
F1 |
T1 |
F1 |
||||||||||||||||||||
F3 |
T3 |
F3 |
||||||||||||||||||||
T1 |
F1 |
F1 |
||||||||||||||||||||
F1 |
F1 |
F2 |
F2 |
F1 |
F2 |
|||||||||||||||||
F2 |
F2 |
F2 |
||||||||||||||||||||
T3 |
F3 |
F3 |
||||||||||||||||||||
F2 |
F2 |
F2 |
||||||||||||||||||||
F2 |
F2 |
F3 |
F3 |
F2 |
F3 |
|||||||||||||||||
| Table 1 : Truth
table for the conjunction: (a ) auxilitary table for the construction of (b); (b ) table of the conjunction |
||||||||||||||||||||||
( c ) |
|
|
T1,3 F1,2 F2,3 |
T1, 3 F1, 2 F2,3 |
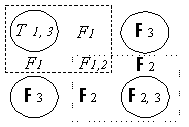 |
| Table 1c) condensed version of table 1b) | |
( a ) |
( b ) |
( c ) |
||||||||||||||
|
T1,3 |
F1,2 |
F2,3 |
X |
N1X |
N2X |
T1,3 |
F1,2 |
F2,3 |
|||||||
| T1,3 | T1,3 |
T1 |
T3 |
T1,3 | F1,2 |
F3,1 |
T1,3 | T1,3 | F1 |
F3 |
||||||
| F1,2 | T1 |
F1,2 |
F2 |
F1,2 | T1,3 |
F3,2 |
F1,2 | T1 | T1,3 |
F3 |
||||||
| F2,3 | T3 |
F2 |
F2,3 |
F2,3 | F3,2 |
F2,1 |
F2,3 | T3 | T3 |
T1,3 |
||||||
| Table 2 : Truth
table for (a) the disjunction, (b) the negations, and (c) the implication. |
||||||||||||||||
Table 1a will help to elucidate the truth table not only for the conjunction, but also for the disjunction, the negations and the implication. Table 1b shows the result for the conjunction, while Table 1c displays a more condensed notation of Table 1b. Table 2 gives the corresponding version for the disjunction, negation and implication, which can be derived very easily with the help of Table 1a.
From these tables, De Morgan´s formulae, for example, for the conjunction and disjunction in a three-contextural system can be deduced, viz.,
|
|
(4) |
|
|
or the relations of contraposition may be formulated:
|
|
(5) |
|
|
For a logical interpretation of McCulloch´s heterarchically structured model describing certain features of nervous activities, this brief survey of some relations will be sufficient. For more details and technical elaboration of the poly-contextural logic, the literaure /16, 17/ should be consulted.
Non-Transitivity
Within the linguistic framework, opened by a three-contextural logic, both transitive and non-transitive relations may be discussed without antinomies and ambiguities.
Intra-contextural, i.e., within the logic of one contexture, the transitivity law holds rigorously, as do the classic logical rules. For the preference represented by relations (1) and (2) one has
|
(6) |
If, for example, the preference relation between the statements A, B and C about the nervous net in Fig. lc is given in three contextures as
| L(3) : | L1 L2 L3 |
|
(7) |
then the transitivity rule holds strictly in each of the three contextures. However, if the implication chain starts in the logical domain L1 (or L2)and continues with a change of the contexture, say in L3 then non-transitivity occurs trans-contexturally in the chain of implication without antinomy, viz.
|
(8) |
Relation (7) may be summarized using (5) as
| L(3) |
|
(7a) |
where L(3) symbolizes the total of three contextures, i.e.,
L(3) = (L1, L2, L3) |
(9) |
and correspondingly for relation (8) it follows from (6) that
|
(10) |
Whereas circularities, which always appear when describing the activities of complex nervous nets, lead to completely meaningless propositions if considered intra-contexturally (i.e., mono-contexturally) they still can be modeled trans-contexturally (i.e., poly-contexturally). In this way linguistic possibilities are developed for a scientifically precise determination of complex notions such as ´self-referentiality´ in which the process of description is distributed over different logical positions of poly-contexturality; finite and operative complexes of ambiguities may be designed.
CONCLUSIONS
The results of modern brain research and the theory of poly-contexturality as a ´general theory of living systems´ indicate the direction of future computer architecture which possibly may be designed on a molecular electronic basis. It. can only be considered a first step that on a molecular level the old ´silicium structures´ in their rigorous binarity are copied and miniaturized simply for purposes of optimizing quantities such as speed, size, etc. For a future computer science, founded on the basis of molecular electronics, the realization of a computer architecture has to be envisaged which models the dialectic and self-referential structure of matter as they appear, for example, in the brain.
Acknowledgment
These studies were supported by a grant from the Stiftung Volkswagenwerk.
REFERENCES
/1/ McCulloch and W. Pitts, Bull.
Math. Biophys. 5,115 (1943) ![]() , 2nd cit.
, 2nd cit.![]()
/2/ H.von
Foerster, Sicht und Einsicht,
Vieweg-Verlag, Braunschweig (1985) ![]() , 2nd cit.
, 2nd cit.![]()
/3/ L.Löfgren, in: Trends in General Systems Theory (edited by
J. Klir), Vol. 3, p.197. Wiley, New York (1977) ![]()
/4/ Maturana and F. J. Varela,
Autopoiesis and Cognition, Reidel, Dordrecht (1972) ![]() , 2nd cit.
, 2nd cit.![]()
/5/ G.Günther, Das
Bewußtsein der Maschinen, Agis-Verlag,
Baden-Baden (1963) ![]()
/6/ G.Günther,
in: Self-Organizing Systems (edited
by M. C. Yovits, G. J. Jacobi and G. O. Goldstein) p. 313,
Spartan Books, Washington, DC (1962) ![]()
/7/ G.Günther, Beiträge zur
Grundlegung einer operationsfähigen Dialektik, Vols 1-3, Felix
Meiner.Verlag, Hamburg (1980) ![]()
/8/ McCulloch, Bull. Math.
Biophys. 7, p.69 (1945) ![]() , 2nd cit.
, 2nd cit.![]()
/9/ McCulloch, in: Embodiments of
Mind, p.387, MIT Press, (1965) ![]() , 2nd cit.
, 2nd cit.![]()
/10/ E.Cohors-Fresenborg,
Mathematik mit Kalkülen und Maschinen, Vieweg-Verlag,
Braunschweig (1977) ![]()
/11/ Varela, in: Principles of Biological Autonomy, North-Holland Publ., Amsterdam. (1979).![]()
/12/ J.Schmidt
(ed.), in: Der Diskurs des Radikalen
Konstruktivismus, Suhrkamp-Verlag, Braunschweig, (1985) ![]()
/13/ Maturana,
Erkennen: Die Organisation und
Verkörperung von Wirkhchkeit, Vieweg-Verlag, Frankfurt, (1987) ![]()
/14/ G.Roth, in: Der Diskurs des radikalen
Konstruktivismus, (edited by S. J. Schmidt), p. 229.
Suhrkamp-Verlag, Frankfurt (1987) ![]()
/15/ Longyear, J. Cybern. 2, p.7 (1972) ![]()
/16/ R.Kaehr, Materialien zur Formalisierung
der dialektischen Logik und der Morphogrammatik, in: Idee und
Grundriss einer nicht-Aristotelischen Logik, (edited by G.
Günther), Felix Meiner-Verlag, Hamburg (1978) ![]() , 2nd cit.
, 2nd cit.![]()
/17/ Kaehr, in:
Die Logik des Wissens und das Problem
der Erziehung, p. 254, Felix Meiner-Verlag, Hamburg (1981) ![]()
| Autoren: R. Kaehr & E. von Goldammer |
|
webmaster@xpertnet.de
Copyright ©: 1996, ICS
last revised Jan. '97