Poly-Contextural Modeling
of Heterarchies in Brain Functions
Rudolf Kaehr and E. von Goldammer
Abstract
All Hebbian rules which are discussed in the literature of neuromorphic nets are embedded within the principle of ultrametricity corresponding directly to hierarchical structures. In order to describe and to model simultaneously distributed parallel neural activities as they occur in heterarchically organized systems (self-referentiality) which cannot be linearized, a formal system for an adequate description of structural circularities and ambiguities is necessary. A basis for such a formal system is given by the theory of poly- contexturality, in which multi-negational operators regulate the duality principles of complementarity, and transjunctional operators produce muiti-simultaneous heterarchical structures.
Introduction
One of the criticisms most often heard about Artifcial Intelligence (AI) is that machines cannot be called intelligent until they are able to learn to do new things and to adapt to new situations, rather than simply doing as they were told to do. There can be little question that adaptibility to new surroundings and to solve new problems is an important characteristics of intelligent entities.
Rather than discussing in advance whether it is possible for computers to "learn", it is more enlightening to try to describe what activities we mean when we say "learning" and what algorithms are necessary to model those activities. One of the very general standard definitions of learning is "a change in performance (for the better, as a function of experience)", a definition which is rather black-box-like and uninformative for the design of any technical device being able to learn.
In the following discussion we will restrict ourselves to a cybernetical description of learning processes as it was discussed, for example, by Bateson (Bateson, 1972) using Russell´s theory of (logical) types as descriptive basis for a classification of different learning processes. Despite of its usefulness and success in various scientific disciplines, Bateson´s model is strongly hampered by the use of the theory of logical types especially if the design of technical entities is envisaged. The shortcomings of this learning model have been discussed elsewhere (von Goldammer & Kaehr, 1989) and will not be repeated here.
The significance of Bateson´s studies is founded methodologically by their logical analysis and description of communication processes such as ´learning´. Keeping the phenomenological part of his classification, we will distinguish between three categories of ´learning´:
Zero learning
Phenomena which approach this degree of simplicity occur in various contexts. A technical example is given by electronic circuits, where the circuit structure itself is not subject to changes resulting from the passage of electrical signals within the circuit, i.e., where the causal links between ´stimulus´ and ´response´ are so to speak ´soldered in´. An intellectually interesting example for ´zero learning´ is the mathematical fiction of a "player" in a Von Neumannian game. Without going into details the essential point of ´zero learning´ is that for this "player" the principle of "trial and error" is excluded, i.e , ´trial and error´ learning does not belong to the repertory of the Von Neumannian "player". Although the meaning of the word ´error´ is not trivial and will be examined below, there is a sense in which the "player" can be wrong. For example, he may base a decision upon probabilistic consideration and then make a move which, in the light of the limited available information, was probably right. When more information becomes available, he may discover that the move was wrong. But this discovery contributes nothing to his future skill, i.e., the discovery that he was wrong in the particular instance has no bearing upon future instances. When the same problem returns at a later time, he will correctly go through the same computations and reach the same decisions. An algorithm for ´zero learning´ in the sense of Bateson´s classification is the ´delta rule´ or ´Widrow-Hoff-rule´ (with a teacher), where the amount of learning is proportional to the difference between the actual activation achieved and the target activation provided by a teacher. In other words, if the entity gives at Time_2 a different response from what it gave at Time_1, the changes (adaption of the system) in this case are caused by a teacher and not by the system itself.
Learning_I or 1st order learning
While ´zero learning´ by definition is charactenzed by specifity of response, which - right or wrong - is not subject to corrections, ´learning_I´ in this terminology is the change in specifity of response by correction of errors of choice within a set of alternatives.
All ´Hebbian rules´ which are discussed in the literature on neuromorphic nets such as the ´Hopfield´-, ´Boltzmann´-, ´Cauchy´-model and others, which originate from physics, belong to the category of ´1st order learning´. These rules are related to changes of the data structure within the learning system. Such processes correspond to Hebb´s principle of self-organisation, i.e., the internal organisation or the data-structure (electrical voltages, currents, etc.) is self-organizing. Thus the behavioristic principle of ´trial and error´ belongs to the repertory of ´1st order learning´. In a cybernetical sense neuromorphic nets are classical I/O-systems with implemented feedback algorithms which are organized ultrametrically (Rammal, Toulouse & Virasoro, 1986). One of the defining relations of metricity is the triangle inequality,
|
(1) |
The notion of ultrametricity is based on the stronger inequality
|
(2) |
A general connection between indexed hierarchies and ultrametrics, which is clearly visible on the classification tree, was rigorously proved by Benzécri (1984). From a logical point of view, ultrametricity directly corresponds to the transitivity relation.
So far all neuromorphic models discussed in the literature lead to ultrametricity, the simplest possible non-trivial organisation of states (Parisi, 1987), and therefore all those nets represent hierarchically structured models. However, there is one exception: the neural nets described ´topo-logically´ by McCulloch in 'A Heterarchy of Values Determined by the Topology of Nervous Nets' (McCulloch, 1945). A detailed logical interpretation of this study has been given elsewhere (Kaehr & von Goldammer, 1988) and will be discussed very shortly in the next sections.
Apart from McCulloch´s nets all other neural models and learning algorithms belong to the field of classical 1st order cybernetics where all the methods of mathematics based on classical logic are sufficient for a formal description and the design of algorithms capable for pattern recognition from a noisy background (´order-from-disorder´). For the field of robotics this situation still corresponds to the case of a ´structured environment´ which is part of the robot controlling program and consequently does not represent an environment from the viewpoint of a robot, i.e., a ´structured environment´ is the label for noisy objects and relations (von Goldammer & Kaehr, 1989).
Learning_II or 2nd order learning
While learning_I in the present classification is a process characterized by correction of errors within a set of alternatives, learning_II is defined (in this terminology) as label for all changes in the process of learning_I. For phenomena of this order various terms have been proposed in the literature of learning theories, such as ´learning to learn´ or ´set learning´ (Harlow, 1949). In the terminology of Bateson, it is the corrective change of the sets of alternatives which distinguishes ´2nd order learning´ form ´1st order learning´ processes where the corrective change occurs within a set of alternatives. More technically spoken. this means that not only the (internal) data structure but also the algorithm, which defines the structure of the system, changes simultaneously during such an autonomous learning process. I.e., for ´1st order learning´ it is the variation of the internal organisation of the data structure which is self-organizing, whereas it is the relationship between the system (e.g., a robot) and its environment which is of self-organizing nature for ´2nd order learning´ processes. This relationship represents a basic requirement for any description of technical or living systems acting, for example, in an ´unstructured environment´. Hence it follows the necessity for any technical design of self-referentiality to model the process of distinction between a system and its environment Therefore ´2nd order learning´ differs basically from ´1st order (adaptive) learning´ as simulated by Hebbian algorithms with their ´causally connected´ way of linkage between domain and internal structure. In a self-referential process an image of the system and its environment is produced by the system itself. viz.,
|
(3a) (3b) |
It is this twofold distinction and hence heterarchical conceptuality which leads to fundamental difficulties if a formal representation for an adequate construction plan of corresponding technical devices is envisaged within the framework of classical logic. Only if the sytem´s representation is restricted to aspects of itself (self- representation of reflective architectures) no logical problems will be produced (cf. ´problems of bootstrapping´; Maes, 1987).
´Learning´ in an ´unstructured environment´ (2nd order learning) comprises at least two simultaneously interacting processes:
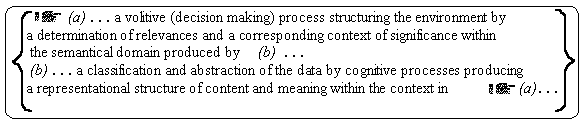
Both processes are complementary to each other, i.e., neither of the two can be considered or described separately. Thus the operator (program) of the volitive process becomes the operand (data structure) of the cognitive system and what has been operator of the cognitive process may change into an operand of the volitive system. Such simultaneously interacting processes constitute a higher order of circularity (´chiasmus´) and parallelism which neither can be reduced to linearity (sequemtial processes) nor can be represented within the linguistic framework of any classical logical system without producing antinomies (circularities). However, computational reflection belongs to the cognitive aspect of behavior whereas volitive aspects usually are neglected.
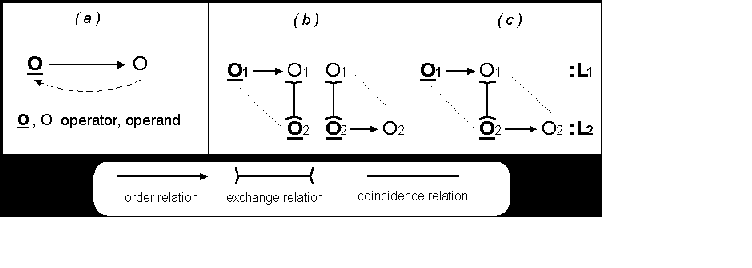 |
| Figure 1: Logical
representation of ´self-referentiality´. ( a ) circularity in a classical mono-logical system; ( b ) distributed circularity on two contextures; ( c ) composition of Fig.1b |
Figure la illustrates the circularity arising within a classical logical representation of self-referentiality as given by relation (3b). This situation results directly from the inversion of the relationship between operator_&_operand and operand_&_operator within one logical system. Thus, there appears no more distinction between operator and operand within the logical domain which is constitutive for any dichotomic system. Following Russell´s paradox, the antinomical situation of this graphic metaphor can easily be logified by the following equations, where circularity is caused by the substitution of O by O0 during the transition from (4b) to (4c):
|
(4a) |
|
(4b) |
|
(4c) |
The correlation between circularlties and antinomies also applies to other examples.
Another way of describing self-referential processes and autonomous systems has been discussed by von Foerster (1984) in connection with the method of indefinite recursion, viz.,
| O1 = O(O0) | |
| O1 = O(O1) = O(O(O0) | |
| . . . |
(5a) |
| On = O(O(O(O(O(O(O ......(O0)))))) | |
| . . . |
|
(5b) |
Hence,
(5c) |
|
(5d) |
The independent variable O0, the ´primary argument´ has disappeared in (5b). O00 expresses an indefinite recursion of the operator O. Any indefinite recursion within expression (5b) can be replaced by O00, as is indicated in (5b), resulting in (5c). If there are values O00,i (i=1,2,... , n) that satisfy eq. (5c) these values are called ´eigen-values´
Ei = O00,i |
leading again to closure as in Fig.la, when the operator is represented by an infinite chain of eigen-values. This is symbolized by eq. (5d). Although this formalism is useful on a descriptive level, it is completely unsuited for an engineering design, because of the central part that ´infinity´ plays as constituent in this representation.
Summarizing in short we are faced with the obvious need of a formalism which allows the description and the engineering design of self-referential processes of autonomous systems, which are characterized by self- organisation between the system and its environment. resulting in heterarchically structured organisations. A theoretical basis for such constructions is provided by the ´theory of poly-contexturality´ representing a formal and operative system of mathematical logic which has been developed first by Günther (Günther, 1980) and was continued in the following by Kaehr (Kaehr, 1981).
Towards cognitive modeling
A ´contexture´ is a logical domain where all classical logical rules hold rigorously. The essential point of ´poly-contexturality´ results from the mediation by order and exchange relations between different (at least three) contextures. Le the logical domains or contextures do not exist in isolation, but are mediated with each other by new and non-classical logical operators, such as for example the ´transjunction´, which allows the modeling of a bifurcation from one logical domain into at least two parallel, simultaneously existing contextures.
In contrast to Fig. la two contextures L1,2 are depicted in Fig.1b in such a way that the relation between the operator and the operand is distributed among two (indexed) contextures. Fig. 1c represents the composition of the distributed relations in Fig. 1b. I.e., circularity is distributed among two logical domains if the meaning of the terms will be retained during the transitions from one domain to another. On the other hand, the relationship between the operators and operands is distributed on two logical domains and therefore it escapes any circularity, provided the individual process will be discriminated during transitions between different contextures. This connection between operator and operand has been called ´proemial-relationship´ (Günther, 1980). Such an interchange, i.e., the distribution and mediation of domains is designated as ´heterarchy´ (heteros = the other and archain = the rule). Heterarchically organized structures or processes belong to the category of autonomous and not to the class of I/O-systems. In the terminology of ´poly-contexturality´, heterarchy is constituted inter-contextural whereas intra-contextural processes are hierarchically structured, which means that intra-contextural, i.e., within the logic of one contexture, the transitivity law holds rigorously, as do all classical logical rules. Thus a parallelism is constituted by a (heterarchically) distributed circularity of the operator and operand which is no longer reducible to linearity (as a process of sequential steps) as it is always possible for the purely hierarchically organized models of neuromorphic nets based on Hebbian learning algorithms.
Since Russell's theory of logical types is exclusively hierarchically structured, no mediation between different equally ranked types exists. Therefore any modeling of simultaneity in the sense as discussed above is ruled out in principle which strongly limitates the technical application of Bateson´s analysis (von Goldammer & Kaehr, 1989).
Poly-contexturality
In the introduction it has already been mentioned that the meaning of the word ´error´ is not trivial especially if it will be used for a description of learning processes. This problem becomes evident for example from the pattern in Fig.2, where the exchange relation causes ambiguity between the logical terms ´true´ and ´false´.I.e. a proposition may be ´true´ in one contexture and ´false´ in another one depending on the respective point of view (context or more precisely contexture).
The scheme corresponds to a three-contextural logical system, the lowest meaningful contexture in the poly-contextural theory. While classical logic is defined between any two values resulting in a contexture, the case with three values, where the third is not placed between ´true´ and ´false´ but beyond ´true´ and ´false´, three two-valued logical systems are generated to which three contextures are assigned.Four values define six logical domains, and in general with m values (m over 2) two- valued logical systems are created. The logical Systems or contextures defined in this way do not coexist in isolation but are mediated with each other, as is reflected by the scheme of a three-contextural system in Fig. 2.
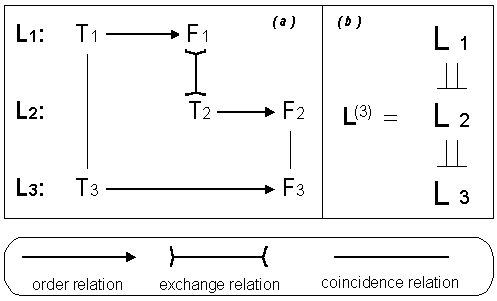
| Figure 2: Three logical contextures: L(3)=
(L1, L2, L3) ( a ) T, true; F, false; ( b ) short notion of the mediation between L1, L2, L3 |
The simultaneity of parallel distributed
processes in poly-contextural systems splits up into two
different types. First there is simultaneity of contextures
without cooperative interactions in between; the contextures,
however, are still mediated with each other. Between the
operators of each contexture, there exist the relationships of
identity, permutation, or reduction. In a three-contextural
system as it is depicted in Fig.2, this is represented in the
following diagrams (7)-(10); secondly, the transjunctional
operator ![]() , which allows the modeling of bifurcation from one
logical domain into at least two parallel simultaneously existing
contextures, will be introduced briefly in the diagram (12). For
better understanding the truth table for the logical operations:
conjunction
, which allows the modeling of bifurcation from one
logical domain into at least two parallel simultaneously existing
contextures, will be introduced briefly in the diagram (12). For
better understanding the truth table for the logical operations:
conjunction ![]() , disjunction
, disjunction ![]() , implications
, implications ![]() , transjunction
, transjunction ![]() ,
and two negations (N1,N2) will be presented. In order to simplify the
notation, the following abbreviations have been introduced:
,
and two negations (N1,N2) will be presented. In order to simplify the
notation, the following abbreviations have been introduced:
{ T1, T3 } := T1,3; { F1, T2 } := F1,2; { F2, F3 } := F2,3 |
(6) |
For more details and technical elaboration of the poly-contextural logic, which cannot be given here, it is referred to the literature (Kaehr, 1981).
Table 1a will help to elucidate the truth table not only for the conjunction. but also for the other operators. Table lb shows the result for the conjunction, while Table 1c displays a more condensed notation of Table 1b. Table 2 gives the corresponding version for the disjunction, negation, implication, and transjunction in L1 (see below), which can be derived very easily with the help of Table la.
( a ) |
( b ) |
|||||||||||||||||||||
L1 |
L2 |
L3 |
L1 |
L2 |
L3 |
|||||||||||||||||
X1 |
Y1 |
X2 |
Y2 |
X3 |
Y3 |
|
|
|
||||||||||||||
T1 |
T1 |
T3 |
T3 |
T1 |
T3 |
|||||||||||||||||
F1 |
T1 |
F1 |
||||||||||||||||||||
F3 |
T3 |
F3 |
||||||||||||||||||||
T1 |
F1 |
F1 |
||||||||||||||||||||
F1 |
F1 |
F2 |
F2 |
F1 |
F2 |
|||||||||||||||||
F2 |
F2 |
F2 |
||||||||||||||||||||
T3 |
F3 |
F3 |
||||||||||||||||||||
F2 |
F2 |
F2 |
||||||||||||||||||||
F2 |
F2 |
F3 |
F3 |
F2 |
F3 |
|||||||||||||||||
| Table 1 : Truth
table for the conjunction: (a ) auxilitary table for the construction of (b); (b ) table of the conjunction |
||||||||||||||||||||||
( c ) |
|
|
T1,3 F1,2 F2,3 |
T1, 3 F1, 2 F2,3 |
|
| Table 1c) condensed version of table 1b) | |
( a ) |
( b ) |
( c ) |
||||||||||||||
|
T1,3 |
F1,2 |
F2,3 |
X |
N1X |
N2X |
T1,3 |
F1,2 |
F2,3 |
|||||||
| T1,3 | T1,3 |
T1 |
T3 |
T1,3 | F1,2 |
F3,1 |
T1,3 | T1,3 | F1 |
F3 |
||||||
| F1,2 | T1 |
F1,2 |
F2 |
F1,2 | T1,3 |
F3,2 |
F1,2 | T1 | T1,3 |
F3 |
||||||
| F2,3 | T3 |
F2 |
F2,3 |
F2,3 | F3,2 |
F2,1 |
F2,3 | T3 | T3 |
T1,3 |
||||||
| Table 2 : Truth
table for (a) the disjunction, (b) the negations, and (c) the implication. |
||||||||||||||||
Permutation
The negational operator N in poly-contextural systems not only negates its logical domain, but also permutates the neighboring contextures:
|
(7) |
|
|
||
| with |
||
X |
|
|
T1 |
F1 |
|
F1 |
T1 |
|
|
(8) |
|
|
||
| with |
||
X |
|
|
T2 |
F2 |
|
F2 |
T2 |
|
Identity
Since NZ1 is a superposition of N1 and N2 it produces identity in the 6th step no matter where one starts; this may be seen from diagram (9).
These relations not only hold for univariate operators but also for bivariate operators.
|
(9) |
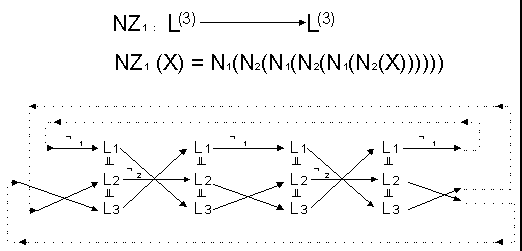
Reduction
Diagram (10) symbolizes that reduction in L2 occurs caused by R1. In anlogy for R2 the reduction is in L3.
|
|
| with | |
|
|
| For disjunction, see Table 2a. | (10) |
|
Transjunction
Cooperative interactions which are modeled by
transjunctional operations in poly-contextural systems are
defined in a way that an operation in one contexture necessarily
involves other operations in the neighboring contextures
initiated by the transjunction which causes a bifurcation of its
own contexture mapping into the neighbored contextures
independently from the operators working in the corresponding
contextures. The corresponding formula with a transjunction ![]()
|
(11) |
is defined in the following diagram (cf. Table 2d):
| with | (12) |
|
|
|
In this case one has a transjunction ![]() in contexture 1 and parallel conjunctions in 2 and 3.
Generally transjunctions together with conjunctions and/or
disjunctions within the neighboring contextures are possible.
in contexture 1 and parallel conjunctions in 2 and 3.
Generally transjunctions together with conjunctions and/or
disjunctions within the neighboring contextures are possible.
Duality principles of complementary in multi-negational systems
Since the poly-contextural logic is a multi-negational system, some laws of multi-negation will be introduced briefly.
two negations and three contextures
negations: 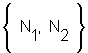 |
|
(13) |
three negations and six contextures
negations: 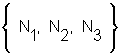 |
|
(14) |
|
cycles of negations
On the basis of the relations (13), (14) and the the substitution rule different cycles of negations can be deduced as for exmple:
|
|
| or | (15) |
Such equivalences are of minor importance for 3-valued systems. For four- and higher-valued systems, however, they take on significance, since it may become important to know whether a certain goal of a reflection process may be reached by different series of negations and which of them are significant.
DeMorgan´s formulae in a multi-negational system
In classical logical systems duality holds intra-contextural as indicated by DeMorgan´s formulae for the disjunction and conjunction:
|
|
|
In transciassical systems there is a distribution of systems of dualities. Multi-duality in poly-contextural systems results from mediation of conjunctions, disjunctions, and negations. For three contextural systems this may be introduced by the following scheme:
| 3 contextures:
|
|
| with | (16) |
|
The duality operators Di are defined through the negations Ni, viz.,
|
|
|
|
|
|
| d1 : duality in L1 | (17) |
|
|
| d2 : duality in L2 | |
| Diagram of a 3-duality of conjunctions and disjunctions: | (18) |
|
For more details and technical elaboration of the poly-contextural logic, which would go beyond the limits of the present study, the literature should be consulted (Kaehr, 1981).
The brain which is a self-referential system par excellence, always interacts with its own states, i.e., it is a completely closed system (Maturana & Varela, 1972). It is this operational closure of the brain functions which implies the problem of circularity (self-referentiality).
The intention of the present contribution was to point to the possibility of modeling in detail cognitive processes without the problem of antinomies. From the viewpoint of poly-contexturality, however, operational closure only represents a phenomenon of secondary interest; it is the distribution, the topology of contextures functions which is of primary significance.
Thus the complement between the operational closure and the topologically distributed brain functions - typical for all heterarchically structured organisations - can be modeled in an adequate way using the theory of poly- contexturality, which is characterized by its distribution and mediation of logical systems.
Acknowledgement
The study was supported by a grant from the Stiftung Volkswagenwerk.
References
Benzécri, J.P. (1984), L´analyse des données 1´, La taxonomie,
Dunond, Paris![]()
Bateson, G. (l972), in: Steps to an Ecology of Mind, Int.Textbook
Publ., London ![]()
Foerster, H. v., (1984), in: Observing Systems, The Intersystems
Inquiring Series, Intersystem Publ. ![]()
Goldammer, E.v. & Kaehr, R., (1989), Lernen in Maschinen und lebenden Systemen, Design
& Elektronik, April 1989, p.146-151 ![]() 2nd cit.
2nd cit.![]() 3rd cit.
3rd cit.![]()
Günther, G., (1980), Beiträge zur Grundlegung einer
operationsfähigen Dialektik, Vol.1-Ill, Felix Meiner-Verlag,
Hamburg ![]() 2nd cit.
2nd cit.![]()
Harlow, H.E., (1949), The Formation of Learning Sets, Physiol.Rev.
56, 51-65 ![]()
Kaehr, R., (1981), in: (Günther, G., eg.) Idee und Grundriss
einer nicht-Aristotelischen Logik, Felix Meiner-Verlag, Hamburg ![]() 2nd cit.
2nd cit. ![]()
Kaehr, R. & Goldammer, E.v., (1988), Again
Computers and the Brain, J.Molecular
Electronics 4, p.31-37 ![]()
Maes, P., (1987), Computational Reflections, PhD-thesis, T.R.,
87-2, AI-Lab., Vrije Universiteit Brussel, Brussells, Belgium ![]()
Maturana,
H.R. & Varela, F.J., (1972),
Autopoiesis and Cognition, Reidel Publ., Dordrecht ![]()
McCulloch, W.S., (1945), A Heterarchy of Values Determined by
the Topology of Nervous Nets, Bull.Math.Biophys. 7, p.89-93 ![]()
Parisi, G., (1987), Facing Complexity, Physica Scripta 35, p.123-124 ![]()
Rammal, R., Toulouse, G. & Virasoro, M.A., (1986), Ultrametricity
for physicists, Rev.Mod.Phys. 58, p 765-788 ![]()
| Autoren: | R. Kaehr and E. von Goldammer |
| published in: | Models of Brain Functions (R.M.J. Cotterill, ed.), Cambridge University Press, 1989, p.483-497 |
webmaster@xpertnet.de
Copyright ©: 1996, ICS
last revised Jan. '97