The Thought Translator

- part 4 of 4 -

"My dear friend", the philosopher answered, "I can answer your question. If one meets a person who is poor or sick, he will always think: This is a thing that may some day happen to me, too. In order to placate the deities which direct his destiny, he opens his purse and heart. But if the same man meets a philosopher he will say: This man is what he is because he is wiser than anybody else. That could never happen to me!" 

I do not think times have changed very much since then. In this article I am going to develop the basic principle of a thought translator. But if I were to go to the Patent Office to obtain protection against later industrial exploitation of my idea, I would certainly be refused. And what an excuse they would have! Remember the story of the fellow who wanted to have his submarine periscope design secured by a patent? He was refused on the ground that his periscope had already been described in Jules Verne's famous novel "Twenty Thousand Leagues Under the Sea." I am afraid I am in the same boat. You've read Lewis Carrol's "Through the Looking-Glass." Remember where Alice steps through a mirror and - we1l, the fourth chapter contains a description of a thought translator! Couched in fairy-tale terms, the description is given as part of the story of Tweedledee and Tweedledum. And here is what you should know about it:

Tweedledee and Tweedledum look exactly alike, but no matter what the first says the other shouts: ,,Contrariwise!" 

This is identical to the logical situation which would arise if two intel1igent races with mutually exclusive mentalities, (that is a human-type mind and a seetee-mind) were to meet each other. In such a theoretical situation, where the human mind is positive, the alien mind must necessarily be negative and vice versa. Accordingly, the chapter about the Tweedle-twins starts out with the following significant lines. Tweedledum addresses Alice, "If you think we are Wax-works you ought to pay. Wax-works weren't made to be looked at for nothing. Nohow!" And Tweedledum adds: "Contrariwise, if you think we're alive, you ought to speak." The alternative of mutually exclusive terms is in this case, of course, dead or alive. Any other total alternative might do as well, but they all boil down to the purely logical one:

it is

or

it is not.

Accordingly, Tweed1edum informs Alice: "If it was so, it might be; and if it were so it would be; but as it isn't, it ain't. That's logic." It is logic indeed! Any logical system we can construct is always a systematic order of tautologies of the general form: if it is, then - and only then - it is. And: if it is not, then - and only then - it is not. There is no doubt Tweedledee knows his logic. On the other hand: to every positive statement his brother makes, Tweedledum bellows, "Contrariwise!" This obviously means that all the statements made by the Tweedle-twins can be separated independent systems which have following forms:

The blanks may be filled with any logical predicate, provided the sequence of predicates is the same in system (I) and (II). Furthermore, both systems must contain an infinite number of statements. So far our two systems seem to differ materially as to what is inside the square. But as Tweedledum and Tweedledee are exactly alike and the only way for Alice to tell them apart is to read the letter sequences "Dum" and "Dee" which are embroidered on their collars, we are going to make the contents of the two systems also alike and merely mark one with a label. This is possible, because if all the conditions for system (II) as given above are fulfilled we are permitted to take the infinite series of "nots" out of system (II) and place a single "not" in front of the "whole" system /1/. Now (I) and (II) are materially exactly alike - like Tweedledum and Tweedledee - but they are total denials of one another. 

This is precisely the situation in which we would find ourselves if we ever met an alien race with a contra-Aristotelian or seetee mentality. Direct spiritual communication is possible between different mental types only so long as their systems of thinking either coincide completely with each other or partially overlap. But all direct intellectual contact must stop if the only relation between two such systems is established by a total negation, which says: there is not one positive truth the aliens have in common with us. 

There is only one way to establish contact - albeit indirectly - between a human and a seetee mentality! This is to design a robot-brain which incorporates a three-valued system of logic. Our mind - let us say it is Tweedledum - and the seetee-mind, represented by Tweedledee, mutually contradict each other in the antithesis of the first two values. But if the robot mind integrates our mutually exclusive two-valued concepts into his three-valued system, my ideas as well as those of the seetee mind will be interpreted in terms of a third value. However, since the human mind is Aristotelian and the seetee mind contra-Aristotelian, each thinking in two-valued terms, the third robotic value will be indifferent relative to the counter-position of the Aristotelian and the contra-Aristotelian system. In other words: if my ideas are transposed into the three-valued system of a robot brain and the same takes place with the concepts of a seetee subject, the third value will turn up in both Aristotelian and contra-Aristotelian logics in a strictly corresponding manner. That means: the two procedures of thinking which are mutually exclusive in a two-valued system do overlap in a three-valued system of robot-mentality. 

In the preceding article - The Soul of a Robot - we demonstrated how a basic logical concept like "AND" was reflected in three different meanings of "AND" within the mental structure of a robot. I shall repeat the necessary tables from "The Soul of a Robot" here.

This table defines our human Aristotelian concept of AND stating that the compound sentence: pANDq is true, and only true, if p and q are independently true. However, if we project this precise logical meaning of AND upon a more comprehensive three-valued pattern of rationality three different meanings of AND do emerge. One which represents the robot concept of AND (· ) a second (· · ) which reflects the seetee meaning of AND within the robotic mentality, and finally a third concept of conjunction (· · · ) which mirrors the way by which the three-valued logic computer interprets our human meaning of AND within his trinitarian system. 

At this point I should like to warn the reader again (as I did in the third article of this series) not to try to "think" the three different meanings of AND as demonstrated in the following truth-table. This is psychologically as well as logically impossible. What the following table shows is the mechanical truth-pattern of a three-valued robot-brain. 

Our own mentality is not three-valued, and if it were, we would not need a thought translator. The situation can be roughly compared to the logical difference between our handling small or very large sums. We can think the results of 1+1 or 1´ 1, but we cannot think 356797351´ 997310971. If we want to know the multiplication result of the two nine digit numbers we have to resort to a mechanical procedure using pencil and paper. Our three-valued table is nothing else hut the governing pattern of some sort of notational arrangement /2/ by dint of which one two-valued (and thinkable) concept is transformed into some other.

As we pointed out before (see my article "The Soul of a Robot") the first truth-function p· q represents the robotic meaning of AND. It represents the thinking proper to the mechanical brain. The truth-function p· · q renders the meaning of AND as it appears in a seetee mind, but projected into a three-valued system. Finally p· · · q repeats our human concept of AND, again transposed into a three-valued pattern. 

It stands to reason that, in order to operate any of these tables, you need negational operators capable of transforming one value into the next one. For our human logic this is done by the Aristotelian negation "~ " The following table indicates that if p has the value 1, then ~ p (non-p) has the value 2, and vice versa.

 This operator is sufficient to handle the two-valued table. However, it is not comprehensive enough to operate the full range of a three-valued table. It cannot perform the step from value 2 to value 3. Our preceding article has therefore introduced a second negation and we will repeat it here for greater convenience. 

Its symbol is ~ ´ and its operational power is defined by the matrix:

This is a strictly contra-Aristotelian negation. We humans cannot perform (think) it. It is part of the hypothetical mentality of a mechanical brain and it indicates the alien thought-processes of a seetee-mind. However; even if we do not use it for our own subjective thought-procedures, we can calculate with it and find out how the mechanical brain translates our concept of AND into the conjunction of the seetee mind and, by a reversal of that process transposes seetee ideas into human concepts. 

This is first done by combining the two independent negations into one three-valued table. We notice that does not operate the value 3, and leaves the value 1 as it is. The comprehensive table has therefore the following appearance:

We have written the values which remain invariant with one negator or the other in italics. Now, look again at the table of the three conjunctions in the mechanical brain. You will find that our human conjunction differs from the seetee concept in all three values. That means: one or the other negational operator is not enough to effect a transformation of our meaning of AND into the corresponding meaning of the seetee world. We shall have to combine both into one single operation. This can be done in two ways. So far we have attached our negations only to positive p. From now on we shall prefix them to our two negated p's. By doing so we obtain the table:

The meaning of this table is that the mechanism first superimposes our thought-process (~ p) upon the negational pattern of the seetee mind (~ ´p) and then reverses the situation by starting from our mental range thereby superimposing the alien pattern of ~ ´ upon our Aristotelian p. Each of these two steps results in a rotational shift of all three values - as seen from positive p. Let's take the first step from p to ~ (~ ´p)! The table shows that value 1 becomes 2. Then 2 shifts to 3, whereas 3 turns into 1. Instead of representing two independent alternatives between 1 or 2, and 2 or 3, the relation of the three values to each other represents a cycle that turns "clockwise" relative to the value-position of p.

The inverse step established by the negational procedure ~ ´(~ p) results in a "counter-clockwise" shift of the values relative to p. That is: from 1 to 3, from 3 to 2, and from 2 back to 1.

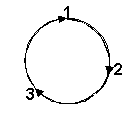
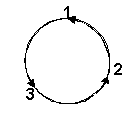
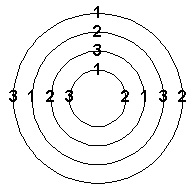
These two rotating wheels which effect an alternative shift of the three values represent the very mechanism of a thought translator. 

This seems to be a brand new idea! Well maybe for cybernetics - but not for Lewis Carroll! Let's get back to the story of Tweedledum and Tweedledee. After having received her lesson about what logic is, Alice looks at the twins, points her finger at Tweedledum, and says, "First' boy." But Tweedledum protests with: "Nohow!" When Alice, passing on to Tweedledee, says, "Next boy," Tweedledee shouts his usual "Contrariwise!" The meaning is obvious: there is no preference between the two, as there can be no preference between an Aristotelian and a contra-Aristotelian way of thinking. But quick-witted Alice gets the point. Consequently, when asked to shake hands she knows she cannot shake hands with either of the twins first, and - so the story continues - "as the best way out of the difficulty she took hold of both hands (each of the twins proffered one) at once: the next moment they were dancing around in a ring." After four rounds they left off. "Four times round is enough for one dance," Tweedledum panted out. 

Caroll has probably chosen the number four for the following reason: you can effect any circular shift of three values by going around in one direction. But when you return to your original position, four "rings" are established. The following figure will demonstrate it:

After the original position has been re-constituted there is no more reason to go "around in a ring." Now Alice and the Tweedle-twins are figures in a story. This article, on the other hand, deals with problems of logic. We shall therefore retain for technical reasons both value-shifts, to the left as well as to the right, because we are now ready to analyze the basic principle of thought translation. The mechanical brain which rotates the values - this is an operation neither our Aristotelian nor the contra-Aristotelian seetee mind can perform - recognizes the fact that both parties, ourselves as well as the aliens, do our thinking in strict alternatives. The first alternative oscillates between 1 and 2, and the second between 2 and 3. But as these alternatives are mutually exclusive and do not overlap, no common ground of communication is possible between them. 

The thought translator, however, transforms these two separate and mutually exclusive alternatives of the Aristotelian and the contra-Aristotelian mind into one and only one equally strict alternative by rotating the three values either "clockwise" or "counter-clockwise." 

The machine produces, so to speak, its own alternative logic of two "values". Only the new "values" are now no longer the individual values 1, 2, and 3, which we have used before, but the two opposite rotational shifts. These shifts partake necessarily in the human as well as the seetee range of thought at the same time. Therefore they permit the translation of human concept into the corresponding seetee meaning - and also the other way round. We shall demonstrate this now with the help of the meanings of the conjunction AND. In doing so we shall indicate the "clockwise" rotation by the new symbol R® and its reversal by R¬ . It is then possible to translate the seetee-concept of AND (p· · q) into the corresponding human reasoning (p· · · q) by the formula:

p· · q º R® (R¬ p· · · R¬ q)

and the seetee intelligence will discover our meaning of AND by using the inverse formula:

p· · q º R¬ (R® p´· · R® q)

Let us see how this is done! We shall use as an example the first of the two formulas. A seetee intelligence says: AND (p· · q), and the thought translator tells us: what the alien thinks is equivalent to the expression: R® (R¬ p· · · R¬ q). Remember that this symbolic figure contains only our concept of conjunction Even so it is not immediately readable for us because the information conveyed to us by the mechanism of the robot-brain is still couched in terms of a three-valued language. In order to understand it we have to reduce it to a two-valued expression. The following table will help to do this:

In our two-valued logic there is only one conjunction p· q and as the Aristotelian system contains only one value-shift, the classical negation ~ , all three-valued negations, no matter what form they have, are reduced to it. Therefore the robotic expression

R® (R¬ p· · · R¬ q)

is now reduced to

~ (~ p· ~ q)

The next table shows us what this fina1 formula means and how we obtain its truth value:

We first write down the values of positive p and q. In column 2 and' 3, we have them negated. In column 5 we establish the conjunction of the negated values. In order to do so either look up the table for AND or just remember that AND has the :value 1 (true) only if both the conjugated concepts have the value 1. The final column, then, results from the negation of column 5. It gives us the final result of what our thought translator has conveyed to us, when we demanded to know what the alien means when he uses the term AND. As we see, the answer boils down to the following juxta-position of meanings - expressed again in a table:

The contra-Aristotelian meaning of AND, however, is our terrestrial meaning of OR (inclusive). Because OR is always true if at least either p or q are true. It is only false in one case - if p and q are both false. I shall leave it to the reader to test the formula.

p· · q º R¬ (R® p· · R® q)

with the same procedure. This formula is the answer which the thought-translator would give to a seetee person, if he (or she) inquired which concept is hidden behind the expression p· · · q. The result would exactly parallel the one we have given above. He (or she) would also arrive at the conclusion that conjunction and disjunction exchange places if we switch from an Aristotelian mentally, and vice versa. 

Let me conclude this series by showing how you can make a crude model of something that works like a thought translator. You require only a small mirror and a certain amount of imagination. First write down your value sequences for conjunction and disjunction in a horizontal line from left to right. But instead of using the word "true" and "false" or the numbers "1" and "2" use some indifferent symbols like ¦ and o Here it is:

¦ o o o

¦ ¦ ¦ o

Then turn your paper with the squares and circles away from you (180 degrees) and step before a mirror. Then look at the reflection of your value sequences in the mirror. In order to interpret properly what you see, you now need a bit of imagination. For you - having an Aristotelian mind - the squares, of course, mean 1 (true) and the circles 2 (false). But do not forget, the contra-Aristotelian mind will interpret them in exactly the opposite way. Do not forget this, and look into your mirror with that knowledge in mind. You will then see that your mirror has turned your conjunction into a disjunction for the other mind, and your disjunction appears as his conjunction. 

Do not try the same experiment with our value-sequences written vertically, as they are placed in our tables. It does not work that way - at least not in this simple manner. You want to know why? Well, the trouble is, you are only looking at your mirror. But when Alice met Tweedledum and Tweedledee she had stepped through the looking glass, and you have no idea how much of a difference that made!

Footnotes:

vordenker Contact: webmaster@vordenker.de
Copyright © Gotthard Günther 1959
Issued: September 2, 1997
Last modified (layout) 2010-12-06